本記事は、2025年に実施された統計検定1級(統計応用・人文科学)問3について、投稿者が作成した解答・解説を掲載しています。
統計検定の問題は、実施団体の規約に基づき当サイトでは掲載しておりません。
出題の正確な内容や公式の解答は、公式問題集や公式サイトの公開情報をご参照ください。
- 記載内容は投稿者個人の見解であり、一般財団法人統計質保証推進協会および日本統計学会の公式見解・公式解答ではありません。
- 内容の正確性には配慮していますが、誤りがあり得ます。ご注意ください。
- 統計検定®は一般財団法人統計質保証推進協会の登録商標です。
[1]
ここで観測変数を$x_1, \dots, x_5$、共通因子を$f_1, f_2$、独自因子を$e_1, \dots, e_5$とし、各因子負荷量を$\lambda_{ij}$とすると
\[
\left(
\begin{array}{c}
x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5
\end{array}
\right)
=
\left(
\begin{array}{cc}
\lambda_{11} & \lambda_{12} \\
\lambda_{21} & \lambda_{22} \\
\lambda_{31} & \lambda_{32} \\
\lambda_{41} & \lambda_{42} \\
\lambda_{51} & \lambda_{52}
\end{array}
\right)
\left(
\begin{array}{c}
f_1 \\ f_2
\end{array}
\right)
+
\left(
\begin{array}{c}
e_1 \\ e_2 \\ e_3 \\ e_4 \\ e_5
\end{array}
\right)
\]
ここで、$\lambda_{ij}$は第$i$変数の第$j$因子に対する負荷量であり、独自因子と共通因子は無相関、因子は標準化されており、分散は1つまり$V(f_j)=1$。
また、これらをベクトルや行列で表すと以下のようになる。
\[
\boldsymbol{x} = \Lambda \boldsymbol{f} + \boldsymbol{e}
\]
ここで、$\boldsymbol{x}$は観測変数ベクトル$\boldsymbol{x} = (x_1, \dots, x_5)’$、$\boldsymbol{f}$は共通因子ベクトル$\boldsymbol{f} = (f_1, f_2)’$、$\boldsymbol{e}$は独自因子ベクトル$\boldsymbol{e} = (e_1, \dots, e_5)’$、$\Lambda$は因子負荷量行列$\Lambda = (\lambda_{ij})$とし$\lambda_{ij}$である。
まず共通性を求める。
ここで、この変数$x_j$の分散$V(x_j)$は次の表せる。
\begin{align*}
\textrm{V}(x_j) &= \textrm{V}(\lambda_{j1}f_1 + \lambda_{j2}f_2 + e_j) \\
&= \lambda_{j1}^2 \textrm{V}(f_1) + \lambda_{j2}^2 \textrm{V}(f_2)
+ 2 \lambda_{j1} \lambda_{j2} \textrm{Cov}(f_1, f_2) + V(e_j)
\\
&= \lambda_{j1}^2 + \lambda_{j2}^2
+ 2 \lambda_{j1} \lambda_{j2} \textrm{Cov}(f_1, f_2) + V(e_j)
\end{align*}
直交解のときは、共通因子同士は無相関つまり$\textrm{Cov}(f_1, f_2) = 0$となっていて、共通性とは共通因子によって説明できる分散のことなので
\begin{align*}
\textrm{V}(x_j)
&= \underbrace{\lambda_{j1}^2 + \lambda_{j2}^2}_{\textrm{共通性 }} + \underbrace{\textrm{V}(e_j)}_{\textrm{独自性 }}
\end{align*}
となり、これより因子負荷量の2乗和$\lambda_{j1}^2 + \lambda_{j2}^2$が共通性の値となる。
これより、ブランドの共通性は
\[
\lambda_{11}^2 + \lambda_{12}^2 = 0.80^2 + 0.40^2 = 0.80
\]
次に接客:$x_2$と因子1:$f_1$の相関係数$\rho (x_2, f_1)$を求める。
このとき、それぞれの分散は1より
\begin{aligned}
\rho (x_2, f_1) &= \textrm{Cov}(x_2, f_1) \\
&= \textrm{Cov}(\lambda_{21}f_1 + \lambda_{22}f_2 + e_2, \; f_1) \\
&= \lambda_{21}\textrm{V}(f_1, f_1)
+ \lambda_{22}\textrm{Cov}(f_2, f_1) + \text{Cov}(e_2, f_1) \\
&= \lambda_{21} \times 1
+ \lambda_{22} \times 0 + 0 \\
&= \lambda_{21}
\end{aligned}
となり、変数と因子の相関係数はその因子負荷量となることがわかる。
これより、
\[
\rho (x_2, f_1) = \lambda_{21} = 0.40
\]
次に接客:$x_2$と品揃え:$x_3$の相関係数$\rho (x_2, x_3)$を求める。
\begin{aligned}
\rho (x_2, x_3) &= \textrm{Cov}(x_2, x_3) \\
&= \textrm{Cov}(\lambda_{21}f_1 + \lambda_{22}f_2 + e_2, \;
\lambda_{31}f_1 + \lambda_{32}f_2 + e_3) \\
&=
\lambda_{21}\lambda_{31}\textrm{V}(f_1) +
\lambda_{22}\lambda_{32}\textrm{V}(f_2) +
\lambda_{21}\lambda_{32}\textrm{Cov}(f_1, f_2) +
\lambda_{22}\lambda_{31}\textrm{Cov}(f_2, f_1)
\\
&\quad
+ \lambda_{21}\textrm{Cov}(f_1, e_3)
+ \lambda_{22}\textrm{Cov}(f_2, e_3)
+ \lambda_{31}\textrm{Cov}(e_2, f_1)
+ \lambda_{32}\textrm{Cov}(e_2, f_2)
+ \textrm{Cov}(e_2, e_3)
\\
&= \lambda_{21}\lambda_{31} + \lambda_{22}\lambda_{32}
\end{aligned}
となる。
なぜなら、各共通因子の分散は1であり、共通因子間は無相関なので共分散は0、また各共通因子と各独自因子と無相関であり、独自因子間は無相関なので。
ここに表1の値を代入すると次の値を得る。
\[
\rho (x_2, x_3) = 0.40 \times 0.90 + 0.50 \times 0.10 = 0.41
\]
[2]
ここで因子分析における寄与率は次のように与えられる。
\[
\textrm{$f_i$の寄与率} =
\frac{\textrm{$f_i$の分散の総和}}{\textrm{$x_i$の分散の総和}}
\]
今回の場合、$f_1$の寄与率は
\begin{align*}
\textrm{$f_1$の寄与率} &=
\frac{\sum_{i=1}^5 \lambda_{i1}^2}{\sum_{i=1}^5 \textrm{V}(x_i)}
\\
&= \frac{0.8^2 + 0.4^2 + 0.9^2 + 0.9^2 + 0.7^2}{1+1+1+1+1}
\\
&= \frac{2.91}{5} = 0.582
\end{align*}
となり、同様にして$f_2$の寄与率は
\begin{align*}
\textrm{$f_2$の寄与率} &=
\frac{\sum_{i=1}^5 \lambda_{i2}^2}{\sum_{i=1}^5 \textrm{V}(x_i)}
\\
&= \frac{0.4^2 + 0.5^2 + 0.1^2 + (-0.2)^2 + (-0.5)^2}{5}
\\
&= \frac{0.71}{5} = 0.142
\end{align*}
[3]
因子分析は観測変数ベクトル$\boldsymbol{x}$を次のように表すことである。
\[
\boldsymbol{x} = \Lambda \boldsymbol{f} + \boldsymbol{e}
\]
このとき、直交回転を行うとは直行行列$H$を使い上記の式を次のように変更することである。
\begin{align*}
\boldsymbol{x} &= \Lambda \boldsymbol{f} + \boldsymbol{e} \\
&= \Lambda I \boldsymbol{f} + \boldsymbol{e} \\
&= \Lambda H H’ \boldsymbol{f} + \boldsymbol{e} \\
&= (\Lambda H) (H’\boldsymbol{f}) + \boldsymbol{e} \\
&= \tilde{\Lambda} \tilde{\boldsymbol{f}} + \boldsymbol{e}
\end{align*}
ここで、$I$は単位行列、$\tilde{\Lambda}=\Lambda H$であり$\tilde{\Lambda}$は回転後の新しい因子負荷行列、$\tilde{\boldsymbol{f}}=H’\boldsymbol{f}$であり$\tilde{\boldsymbol{f}}$は回転後の新しい因子ベクトルである。
このとき、回転後の共通性は回転前と同じであり、直交回転のとき回転後の因子同士も分散が1で相関が0となっている。
なぜなら、共通性は$\tilde{\Lambda} \tilde{\Lambda}’$の対角成分となるので
\[
\tilde{\Lambda}\tilde{\Lambda}’ =
(\Lambda H) (\Lambda H)’ =
\Lambda H H’ \Lambda’ =
\Lambda \Lambda’
\]
となり、$\Lambda \Lambda’$の対角成分と一致することがわかる。
また、$\tilde{\boldsymbol{f}}$の分散共分散は
\[
\textrm{V}(\tilde{\boldsymbol{f}}) =
\textrm{V}(H’\boldsymbol{f}) =
H’ \textrm{V}(\boldsymbol{f}) H =
H’ I H = H’H=I
\]
となり、分散が1で相関が0となっていることがわかる。
以上より、(B)の値を求める。
まず表2における(A)の値は表1で求めた値と一致するので$\textrm{(A)} = 0.80$であり、(B)は次の式から求められる。
\begin{align*}
0.40^2 + \textrm{(B)}^2 &= 0.80 \\
\textrm{(B)}^2 &= 0.64 \\
\textrm{(B)} &= \pm 0.8
\end{align*}
となり、数値的には$\textrm{(B)} = \pm 0.8$となるが他の変数の因子負荷量をみるとすべて正の値であり他の観測項目との評価からも$\textrm{(B)} = 0.8$とした方が解釈しやすくなる。
[4]
斜交回転における$f_1$と$f_2$の相関係数は次のように求められる。
ここでは品揃え:$x_3$で考える。
\begin{align*}
\textrm{V}(x_3) &= \textrm{V}(\lambda_{31} f_1 + \lambda_{32} f_2 + e_3) \\
&=
\lambda_{31}^2 \textrm{V}(f_1) + \lambda_{32}^2 \textrm{V}(f_2)
+ \lambda_{31} \lambda_{32} \textrm{Cov}(f_1, f_2)
\\
&\quad
+ \lambda_{31} \textrm{Cov}(f_1, e_3)
+ \lambda_{31} \textrm{Cov}(f_2, e_3)
+ \textrm{V}(e_3)
\\
&=
\lambda_{31}^2 + \lambda_{32}^2
+ \lambda_{31} \lambda_{32} \textrm{Cov}(f_1, f_2)
+ \textrm{V}(e_3)
\end{align*}
これより、
\begin{align*}
\textrm{V}(x_3)
&= \underbrace{
\lambda_{31}^2 + \lambda_{32}^2
+ \lambda_{31} \lambda_{32} \textrm{Cov}(f_1, f_2)
}_{\textrm{共通性 }} + \underbrace{\textrm{V}(e_3)}_{\textrm{独自性 }}
\end{align*}
このとき変数「品揃え」について、共通性$0.82$、因子1負荷量$0.66$、因子2負荷量$0.410$を代入すると
\begin{align*}
0.82 &=
0.66^2 + 0.410^2 + 2\times 0.66 \times 0.410 \times \textrm{Cov}(f_1, f_2)
\\
\textrm{Cov}(f_1, f_2) &=
\frac{0.82 – 0.66^2 – 0.410^2}{2\times 0.66 \times 0.410}
\approx 0.40
\end{align*}
となり、ここで$f_i$の分散は1より$f_1$と$f_2$の相関係数は
\[
\rho (f_1, f_2) = \textrm{Cov}(f_1, f_2) \approx 0.40
\]
[5]
いま元の変数の分散は1となっているので、独自因子の分散は次のように与えられる。
\[
\textrm{独自因子の分散} = 1 – \textrm{共通性}
\]
これから、各変数の独自因子の分散は次のように与えられる。
\begin{align*}
\textrm{ブランド}&: 1 – 0.80 = 0.20\\
\textrm{接客}&: 1 – 0.41 = 0.59\\
\textrm{品揃え}&: 1 – 0.82 = 0.18\\
\textrm{味}&: 1 – 0.85 = 0.15\\
\textrm{価格}&: 1 – 0.74 = 0.26
\end{align*}
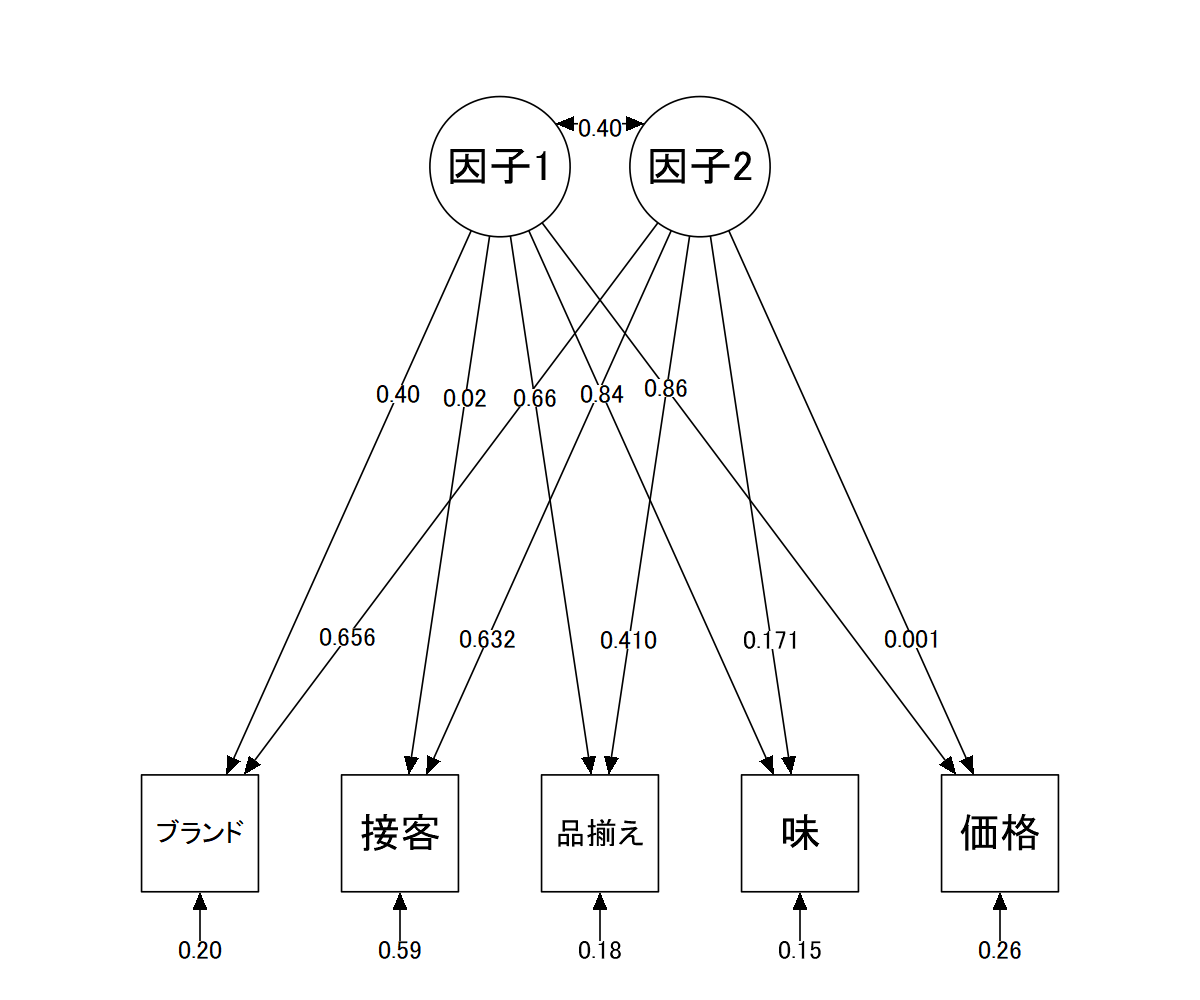
これより、パス図は以下のようになる。